Introduction
The frequency waveform generator WG is set to the resonant frequency of the Piezo, for maximum sound output. This is around 3500Hz, and is very shrill.
The compressions and expansions of the Piezo generate high and low pressure regions in front of it, which travel at the speed of sound, which in air at 25 degree celcius is around 340m/S .
The microphone digitizes the pressure and plots it as a function of time. Since the applied waveform is sinusoidal, the detected signal will also be sinusoidal in shape.
However, Since the compressions and rarefactions of air take some time to reach the microphone, there will be a phase difference between the applied signal
and the received signal.

The oscilloscope monitors two signals:
- the sine wave driving the Piezo. This is done by connecting WG output to A1.
- and the signal detected by the microphone.
It is triggered by the sine wave driving the Piezo
When the microphone is moved, the phase difference between the two waveforms changes.
For half wavelength the phase difference is 180 degree. A connection diagram is shown below.


Screenshot
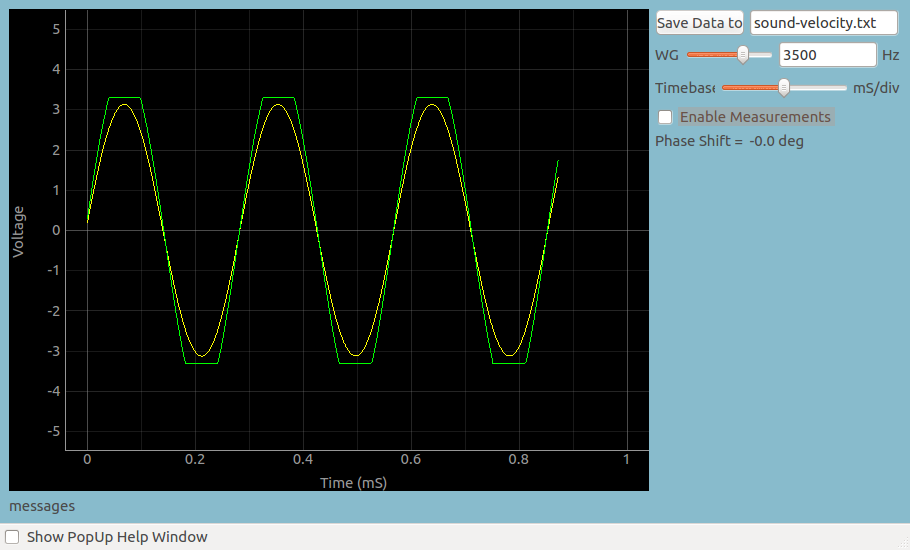
The microphone-piezo distance is adjusted such that the two waveforms are in phase(overlapping) . The exact phase difference is also calculated
using a sine fit, and shown on the right side.
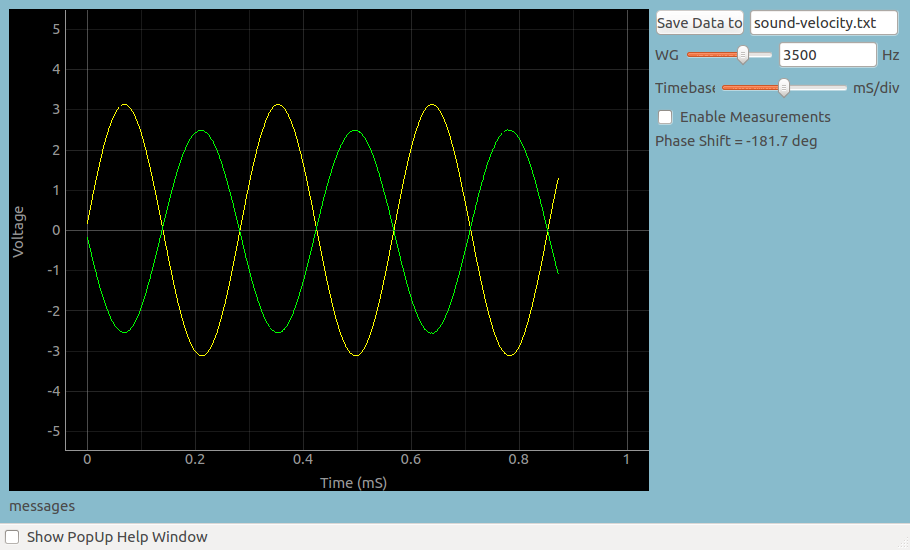
Out of phase condition
Now slowly increase the distance until the phase difference is 180 degrees. This distance is equal to the distance between a compression and rarefaction as shown in Figure 1.
Analysis
The change in distance ‘d’ is measured. This only half the total wavelength
the velocity of sound is given by: v = 2 * d * 3500(frequency of the sound)
You may also attempt the same by measuring 360 phase shift instead of 180.
See Also
 Jithin B.P.
Jithin B.P.




